1. 서론
인간은 음성을 발화하기 위해서 혀와 입술과 같은 조음기관(articulators)을 시공간적으로 정교하고 복잡하게 움직여야 한다(Browman & Goldstein, 1986, 1992, 1995). 이러한 운동을 조음(articulation)이라 칭하며, 인간의 운동 중 가장 빈번하고 중요한 운동이다. 하지만 조음 운동의 많은 부분이 눈으로 볼 수 없는 구강 내에서 일어나기 때문에 음향 데이터에 비해 데이터 수집이 어렵고 높은 비용을 치러야 한다(Nam, 2011). 이런 이유로 국내의 조음 연구는 그 중요성에 비해 활발하지 않았다(Hwang, 2019; Son, 2020). 본고에서는 조음의 로보틱스에 대한 연구 방법론을 소개함으로써 조음에 대한 인지적, 물리적 이해를 더하고, 향후 말하는 로봇 개발 연구에 그 이론적 기반을 제공하고자 한다.
2. 조음 Task와 기본 요소 매핑
조음 기관의 움직임, 즉 조음은 인간 움직임(action)의 한 형태이므로 조음을 이해하기 위해선 인간 움직임에 대한 이해가 반드시 선행되어야 한다(Saltzman & Munhall, 1989). 인간의 움직임은 주어진 목표(task 혹은 goal)를 성취하는 과정으로 이해할 수 있는데, 그 움직임에 필요한 기본 요소는 다양한 수준으로 구분 가능하다(예: 뼈, 근육, 신경 등). 즉, 하나의 움직임 task는, 뼈의 수준에서, 근육의 수준에서, 혹은 신경 체계의 수준에서 설명 가능하다. 하나의 움직임 task를 성취하기 위해 각 수준(예: 뼈)의 다수의 요소들은 서로 협업(synergy)하게 된다. 이때 보통은 task를 성공적으로 달성하기 위해 필수적으로 요구되는 수(degrees of freedom) 이상의 요소가 관여된다. 예를 들어 앞에 놓인 컵을 잡는 것은 어깨 관절만 움직여도 달성할 수 있는 task이지만, 대개의 경우 어깨뿐 아니라 팔꿈치, 손목, 허리까지 움직이기도 한다. 이런 요소 수의 과잉(redundancy) 때문에 인간의 움직임은 같은 task임에도 불구하고 다양한 방법의 움직임이 가능하다. 이러한 문제를 이해하는 것이야말로 인간 움직임의 이해에 대한 가장 큰 난제이며 로봇 제어의 핵심이기도 하다(Bernstein, 1967).
조음은 대표적인 인간의 움직임 중 하나로서 다른 인간의 움직임과 마찬가지로 task와 기본요소들의 관계로서 이해할 수 있다(Browman & Goldstein, 1986, 1992, 1995). 그림 1은 성도(vocal track) 상에 존재하는 다섯 개의 서로 다른(discrete) 조음 기관(입술, 혓끝, 혓몸, 연구개, 성문)과 각 기관에서의 task를 정의하고 있다. 조음이라는 task는 각 조음 기관에서의 성도 협착(vocal tract constriction)을 위한 움직임으로 이해할 수 있다. 이러한 움직임은 두 가지로 다시 나뉘는데 어느 정도의 협착을 하는지(constriction degree) 그리고 그 협착이 정확히 어느 위치인지(constriction location)가 그것이다. 단 연구개와 성문은 그 위치가 고정되어 있으므로 위치에 대한 움직임은 필요치 않다. 그림 1에서 보듯이 입술(lips)과 혓끝(tongue tip)과 혓몸(tongue body)에서의 움직임 task는 협착 위치와 협착 정도로 구분된다. 즉, 입술에선 lip aperture(LA)와 protrusion(PRO), 혓끝에선 tongue tip constriction location(TTCL)과 tongue tip constriction degree(TTCD), 혓몸에선 tongue body constriction location(TBCL)과 tongue body constriction degree(TBCD)로 구분된다. 연구개와 성문에의 task는 각각 velum(VEL)과 glottis(GLO)로 명명한다.
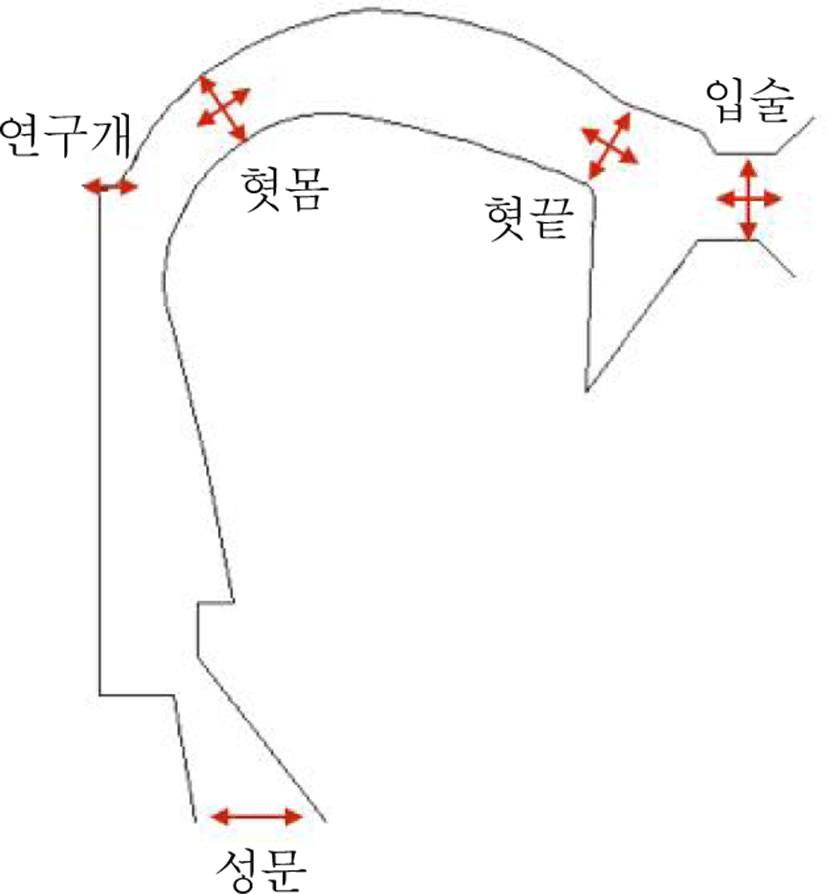
이렇듯 조음은 성도 상에 존재하는 각 조음 기관에서의 협착이라는 움직임 task를 성취하는 과정으로 이해할 수 있다. 이러한 조음 task를 성취하기 위해서 신체의 다양한 수준(예: 뼈, 근육, 신경 등)에서의 기본요소들이 관여하는데 본고에서는 근육과 신경을 제외한 로봇 제어에 필요한 기본 요소인 joint 변수에 국한하기로 한다. 그림 2는 Mermelstein(1973)이 제안한 대표적인 조음 모델로서, 대부분의 로봇 제어에서처럼 기본요소를 joint로 정의하고 있다.
먼저 턱(J)은 관절융기(condyle)로부터 고정된 길이의 segment인 FJ에 의해 연결되어 있다. 턱의 위치는 수평선을 기준으로 정의된 JA에 의해 결정된다. 혓몸(tongue body)은 BC를 반지름으로 하는 원으로 정의되고, 턱과 마찬가지로 그 원의 중심인 C 또한 condyle 뼈에 연결(FC)되어 있다. C의 위치는 J의 위치, 즉 FJ에서부터 상대적 관절각(joint angle)인 CA에 의해 결정된다. CA뿐만 아니라 FC 또한 변동 가능하여 C 위치를 결정짓는다. 요약하면, C의 위치는 JA, CA, FC에 의해 결정된다. 여기서 요소수의 과잉의 문제는 다시 대두된다. 혓몸의 위치(C)를 표현하는데 필요한 자유도는 2차원(x, y)인데, 혓몸의 위치는 3개의 요소(JA, CA, FC)가 개입한다. 이러한 요소수의 과잉은 현실에서 동일한 말을 함에도 턱을 많이 쓸 수도 그러지 않을 수도 있음으로 나타난다. 혓날(tongue blade, BT)은 혓몸 원과 FJ가 만나는 점으로부터 반시계 방향으로 0.55π의 위치(B)에서 혓끝(T)까지의 팔로서 정의된다. 혓끝의 위치는 변동 가능한 길이의 BT와 수평선을 기준으로 정의된 TA에 의해 결정된다. 윗입술과 아랫 입술은 상하 운동이 가능하며 각각 UH와 LH로 정의된다. 여기서 FC와 BC는 변수의 일관성을 위해 CL, TL로 부른다. Joint 변수 중 JA, CA, TA는 revolute joint이고, UH, LH, LX는 prismatic joint이다. 일반적으로 대부분의 로봇은 segment는 변수가 아닌 고정된 값이고, joint만이 변수이다. 반면, Mermelstein 조음 모델은 joint뿐 아니라 segment 또한 변수가 된다(예: CL, TL). 이것은 사람 혹은 로봇의 팔과 같은 모델과는 달리 인간의 조음기관이 그 길이가 변할 수 있는 근육수화기(muscular hydrostat)라는 점을 반영한 결과라고 볼 수 있다. 본고에서는 편의상 segment 변수 또한 joint 변수라고 칭하겠다. Mermelstein 모델이 조음 운동과 관련된 기본 요소를 완벽하게 모델링한다고 할 수는 없지만 조음의 운동 원리를 이해하는 데 필요한 최소한의 기본요소를 갖추고 있다.
조음 운동 원리에 대한 이해는 조음 task 변수들과 joint 변수들 간의 관계를 이해함으로써 비로소 가능해지고, 로봇공학적 구현과 밀접한 관계가 있다. 표 1은 task 변수와 joint 변수와의 관계를 나타낸다. 각 task 변수에 대해서 어떠한 joint 변수가 관여되어 있는지를 보여 준다.
| LX | UH | LH | JA | CL | CA | TL | TA | NA | GW | |
|---|---|---|---|---|---|---|---|---|---|---|
| PRO | ○ | |||||||||
| LA | ○ | ○ | ○ | |||||||
| TBCL | ○ | ○ | ○ | |||||||
| TBCD | ○ | ○ | ○ | |||||||
| TTCL | ○ | ○ | ○ | ○ | ○ | |||||
| TTCD | ○ | ○ | ○ | ○ | ○ | |||||
| VEL | ○ | |||||||||
| GLO | ○ |
표 1에서 볼 수 있듯이 모든 task 변수가 모든 joint 변수와 연관되어 있지는 않다. 입술 움직임의 수평적 움직임에 해당하는 task인 PRO는 joint 변수인 LX만 수반한다. 반면, 입술 열림(LA) 해당하는 task인 LA는 joint 중 UH, LH, JA에 의해서 구현 가능하다. JA는 PRO, VEL, GLO를 제외한 모든 task에 관여된 것을 알 수 있다. 또한 CL과 CD는 혓몸 task인 TBCL, TBCD뿐 아니라 혓끝 task인 TTCL, TTCD에도 관여되어 있다. 혓끝 task인 TTCL, TTCD는 혓몸 task인 TBCL, TBCD에 수반된 joint에 더하여 TL, TA 또한 필요로 한다. VEL과 GLO는 PRO와 더불어 task와 joint간 일대일 대응으로 정의되어 있다.
3. 조음 동역학(Task dynamics)
2장에선 성도상 5개의 조음기관에서의 task를 정의하고 각 task가 조음 모델의 어떤 joint들과 연계되어 있는지 알아 보았다. 3장에선 이러한 task와 joint간의 매핑을 기반으로 어떻게 조음의 운동이 로보틱스의 관점에서 이루어질 수 있는지 알아 본다(Kay, 2003). 즉, 특정 task에 대해 목표값이 주어졌을 때 어떻게 말하는 로봇이 움직이는지에 대한 원리를 알아본다. 더 구체적으로 task와 joint 변수가 시간에 따라 어떻게 변할지를, 즉 task와 joint의 위치와 속도를 시간의 함수(time function)로 계산한다.
그림 3, 4는 각각 2관절 팔 시스템에서의 task와 joint에 대한 정의이다. 2관절 팔 시스템은 인간의 팔 움직임을 구현하는 가장 단순한 모형으로서 두개의 segment(L1, L2)를 가지고 있고 joint인 어깨(shoulder)와 팔꿈치(elbow)로 이루어져 있다. 이 로봇에게 그림 3처럼 세로의 직선을 하나 긋게 하는 task가 주어진다면 그림 4에서의 로봇 joint를 어떻게 움직여야 하는지는 그렇게 단순한 문제가 아니다. 대부분의 경우 task는 인간의 관점에서 주어진다. 세로의 직선을 긋는다는 것이 인간의 관점에서는 평범해 보이지만 로봇의 관점에서는 어깨 관절과 팔꿈치 관절을 적절히 움직여 손끝에서 직선이 그어지도록 해야 하는 복잡한 작업이다. 마찬가지로 이런 문제는 인간에게도 쉬운 문제가 아니다. 인간은 인지적으로 단순히 세로 직선을 긋는 명령을 하고 수행하는 것처럼 보이지만, 개별 joint를 어떻게 움직여야 하는지를 고려해야 한다면 결코 쉽지 않은 문제다.
그림 3에서처럼 많은 경우 인간의 관점에서의 task는 데카르트 좌표(Cartesian coordinates) 상에서 로봇 시스템의 끝점(end-point)에 의해 정의된다. 대부분의 task가 팔의 끝인 손으로 수행되지 팔꿈치로 수행되는 경우는 드문 것으로 이해하면 된다. 반면 로봇 관점에서의 joint는 그림 4에서와 같이 극좌표(polar coordinates) 상에서 정의된다. 이러한 task-joint 관계는 조음의 그것과 동일하다. 다만, 조음의 task- joint 관계는 8개의 task 변수와 10개의 joint 변수로, 2관절 팔 시스템은 두 개의 task 변수 x1과 x2로, 두 개의 joint 변수 θ1, θ2로 정의된다.
자연스러운 움직임을 모델링하기 위해선 고전 역학에서 밝혀진 운동 법칙을 기반으로 한 운동 방정식을 이용할 수 있다(Saltzman & Munhall, 1989). Task 변수, joint 변수 둘 다 운동 방정식으로 그 움직임을 정의할 수 있는데, 일반적으로 task가 인간의 관점에서 제어하는 대상이므로 task 변수를 중심으로 운동 방정식을 정의한다. m개(여기서 2개)의 task 변수(여기서 x1과 x2)에 대해서 식 (1)과 같이 2차 미분 방정식의 형태로 정의된다.
ẍ, ẋ, x, x0 는 m×1(여기서 2×1) 벡터로서 task 변수의 가속도, 속도, 위치, 목표값이고, M, B, K는 m×m(여기서 2×2) 대각행렬(diagonal matrix)로서 질량(mass), 감쇠(damping), 탄성계수(stiffness)에 해당된다. 이 때 M, B, K를 대각행렬로서 설정함은 task 변수 간 서로 연계되지 않음(uncoupled)을 의미한다. 구해진 해에 대해서 task 초기값, 즉 ẋ, x이 주어지면 움직임을 생성하게 된다.
하지만, 이 운동 방정식만으로는 task의 움직임을 정의하는 것이지 로봇의 변수인 joint를 제어하는 것은 아니다. 즉 시스템의 끝점의 움직임만 정의했을 뿐 로봇이 실제 어떻게 움직여야 하는지에 대한 joint의 움직임에 대해서는 관여하고 있지 않다. 다시 말하면, 인간의 관점에서의 움직임, 즉 task의 움직임에 대한 정의만 되어 있고, 로봇의 관점에서의 움직임, 즉 joint의 움직임에 대한 정의는 되어 있지 않다. 이와 같이 운동 방정식을 통한 움직임의 정의는 task 수준에서만 하고 joint 움직임, 즉 joint의 운동학은 task로부터 변환가능하다. 표면적으로는 운동방정식을 통하여 인간의 관점인 task 변수를 제어하고 task와 joint 사이를 연결시킴으로써 궁극적으로는 로봇을 제어하는 시스템이 완성된다. 이러한 task와 joint의 연결을 위해선 운동 방정식에 나타나는 task 변수인 ẍ, ẋ, x를 로봇의 joint 변수인 , , θ로 표현해야 한다. 식 (2)~(4)의 task와 joint간의 운동학적 관계를 이용하여 task 변수를 joint 변수로 변환한 뒤 task 변수로 정의된 운동 방정식을 joint 변수로 정의된 운동 방정식으로 바꿔주면 된다. 이러한 운동학적 변환을 거쳐서 결국 로봇 변수를 제어하는 동역학 시스템이 구현된다.
먼저 task 변수 x는 joint 변수 θ의 함수로서 식 (2)와 같이 정의되고 포워드 운동학 모델이라고 한다. x는 m×1(여기서 2×1)의 벡터이고 θ는 n×1(여기서 2×1)의 벡터이다. 고정된 길이의 segment와 joint의 값이 주어졌을 때 끝점의 위치는 다음과 같이 삼각함수의 공식으로 쉽게 계산된다.
다음 과정으로, 각각의 joint 변수의 변화량에 대한 joint의 함수인 각각의 task 변수의 변화량을 정의해야 한다. 이러한 다변수 편미분(partial derivative) 행렬을 Jacobian 행렬이라 한다(Saltzman & Munhall, 1989). 이때 joint의 값에 따라 편미분 값은 변하므로 Jacobian 행렬을 joint의 함수라고 할 수 있다. 또한 Jacobian 행렬은 joint와 task의 가장 필수적 매핑으로 포워드 운동학 모델이 명시적 공식으로 존재하면 쉽게 편미분 도출 가능하다. 하지만, 모델의 구조(예: segment, joint)가 명시적이지 않은 시스템의 포워드 동역학 모델은 공식으로 존재하지 않기 때문에 Jacobian 행렬은 데이터로부터 경험적으로 구할 수밖에 없다.
Jacobian 행렬이 정의되면 연쇄법칙(chain rule)을 이용하여 식 (3), (4)와 같이 ẋ 를 joint 변수로 표현하고 다시 미분하여 ẍ를 joint 변수로 변환한다. 사실상 Jacobian 행렬만 알고 있으면 기본적인 task 수준의 로봇의 제어가 가능하다. 즉, 어떤 task가 주어졌을 때, joint가 어떻게 움직여야 하는지가 계산 가능하다. 예를 들어 joint 변수와 task 변수의 현재 값을 알고 있을 때 task 변수의 목표값이 주어진다면, Jacobian은 주어진 task 변수의 목표에 대해 joint 변수가 어떻게 움직여야 성취되는지에 대한 선형 근사치를 줄 수 있다. J가 joint(θ)의 함수이므로 joint 변수값에 따라 변한다. 위의 식은 현재의 joint 변수값(θ)대해 목표값의 방향으로 현재의 task를 조금 움직이기(δx) 위해서 현재의 joint를 얼마나 변화(δθ)시켜야 하는지를 말해 준다. 더 구체적으로 Jacobian을 통한 제어는 다음과 같다. 포워드 운동학 모델을 이용하여 현재의 joint 상태로부터 현재의 task 상태를 구한다. Task의 목표값의 방향으로 δx를 정해주면 움직여야 할 joint의 δθ가 얻어지고 이 δθ를 현재의 θ에 더 해주면 된다. 이러한 과정을 task의 목표값이 달성될 때까지 반복해 주면 된다. 이 때 δx가 너무 크게 되면 추정된 선형 근사치 오차가 커지게 된다. 이러한 방식으로 주어진 task에 따라 로봇을 제어할 수 있지만, 질량과 힘이 무시되고 속도가 동일하기 때문에 task 변수, 즉 끝점의 움직임이 자연스럽지 못하다.
식 (1)의 task 기반 운동 방정식은 식 (2)~(4)에서 정의된 task와 joint 변수간의 kinematic 관계식을 이용하여 식 (7)의 joint 기반 운동 방정식으로 변환된다(Saltzman & Munhall, 1989).
이 때 이 운동 방정식의 변수는 task 변수인 ẋ, ẍ, x이 아니라 joint변수인 , , θ로만 정의되어 있다. 하지만 시스템을 통제하게 될 계수인 M, B,K,x0, J, 는 task 관점의 매개변수이다. 즉, 이렇게 함으로써 인간 관점의 task 명령을 내리면 joint 기반 운동방정식으로 로봇 제어가 가능해진다. 이러한 joint 기반 운동방정식은 ODE solver를 통해 그 해인 joint를 구할 수 있고 다음의 과정으로 요약된다.
먼저 joint 초기값으로 , θ이 주어져 있다고 가정할 때 forward kinematics 모델은 ẋ, x를 계산한다. ẋ, x는 forward dynamics 모델을 통하여 ẍ를 구한다. 이렇게 구해진 ẍ, ẋ, x과 joint-task관계 kinematics를 이용하여 도출된 위의 joint기반 운동 방정식은 다음의 timepoint의 , θ를 구하게 된다. 이러한 과정을 반복하여 로봇의 움직임 전체가 계산된다.
조음 동역할 모델을 완성하기 위해서 3.1절의 2관절 팔 시스템의 두 개의 task와 두 개의 joint 변수의 관계를 2절에서의 8개의 조음 task와 10개의 joint 변수로 대체하기만 하면 된다. 먼저, forward model은 그림 2의 Mermelstein 모델에서 정의된 joint 변수로부터 삼각함수를 기반으로 task를 계산할 수 있다. 앞서 언급했듯이 Jacobian matrix는 포워드 모델, 즉, joint 변수에서 조음 task로의 변환 모델이 명시적인 함수의 형태로 주어졌을 경우 편미분을 통하여 쉽게 도출 가능하다. 식 (6)의 2관절 팔 시스템에 쓰였던 2×2 Jacobian matrix는 8×10의 차원으로 확대된다. 표 1은 사실상 Jacobian matrix에서 0이 아닌 요소를 나타내고 있다. 조음 동역학 구현을 위한 나머지 과정은 2관절 팔 시스템에서와 동일하다.
4. 논의 및 결론
본고의 말하는 로봇은 결국 조음 합성기(articulatory synthesizer)를 만드는 것을 의미한다. 조음 합성은 음성 합성(speech synthesis)의 한 분야로서 높은 비용과 낮은 성능 때문에 상업적으로 이용되지는 못 했다. 그러한 한계에도 불구하고 조음 합성은 음성의 발화 및 지각의 원리를 있는 그대로 연구하는 과학으로서 가치가 있다. 대신 조음의 과정을 무시한 연결 합성(concatenative synthesis)이나 통계기반 파라미터 합성(statistical parametric synthesis)이 상업과 실용의 영역을 대신해 왔다. 특히 최근에는 딥러닝(deep learning) 기반의 음성 합성이 성능이나 비용에서 탁월한 성과를 보이고 있다(Shen et al., 2018).
말하는 로봇을 만든다는 것은 음성 발화의 계획(planning), 조음기관의 동작, 음성 출력의 생성 등 각각의 독립된 모델의 개발을 의미한다. 본고는 그 중 조음기관의 동작 모델에만 국한했다. 또한 본고는 위치, 속도, 가속도의 kinematics만을 구현하는데 초점을 맞추었음을 밝혀둔다. 실제 질량을 가지고 있는 로봇을 구동하기 위해서는 계산된 운동학으로부터 그 필요한 힘(force, torque)을 역계산해야 한다. 이 과정을 inverse dynamics라고 하고 본고에서는 다루지 않았다. 또한 조음기관이 동작하기 위해선 음성 발화의 계획이 필요하다(Nam & Saltzman, 2003; Nam et al., 2004). 조음기관의 동작 단위를 음성 gesture라고 부르는데 하나의 gesture는 어떤 조음 기관을 사용하는지, target, stiffness, 시구간(time interval) 같은 정보가 정의되어야 한다. 예를 들어 /b/라는 음소를 내기 위해서는 LA gesture가 필요한데 target은 0 mm, stiffness는 8 Hz의 속도를 가진 gesture가 80msec 동안 활성화(activation)한다는 정보를 부여해야 한다. Gesture은 서로서로 시간적 overlap이 가능하다. 즉, 한 조음기관이 동작하는 동안 다른 조음기관이 움직일 수 있다. 이러한 gestural overlap은 동시 조음(coarticulation)의 기저 원리가 된다(Fowler & Saltzman, 1993). 이렇듯 한 단어를 제대로 발화하기 위해서는 여러 조음 기관에서의 gesture들을 시공간적으로(spatiotemporally) 적절히 어울러야 한다(coordination). 이러한 음성 발화의 계획을 입력으로 조음 기관이 움직이게 된다. 조음 기관이 움직이면서 변화하는 성도(vocal tract) 단면적(area function)은 성대에서 만들어진 voice source에 filter 역할을 한다. 순간순간의 성도 단면적으로부터 생성된 짧은 소리가 순차적으로 연결됨(temporal concatenation)으로써 최종의 음성 발화가 가능하게 된다.
국내의 조음 연구는 그 중요성에 비해 미비한 선행 연구, 고가의 연구 비용 등의 문제로 활발하게 이루어지지 않고 있다. 본고는 음성 발화의 시작이 되는 조음을 운동학, 동역학, 로보틱스의 관점에서 재조명함으로써 조음의 원리를 이해하는 데 도움을 주고자 했다. 또한 인공지능으로 대변되는 4차 산업혁명시대에 실제 조음기관을 가진 로봇의 개발이 이루어지길 기대하며 본고가 그 촉매제 역할을 하길 기대한다.










