Modified AWSSDR method for frequency-dependent reverberation time estimation

Kim, Min Sik; Kim, Hyung Soon

doi:10.13064/KSSS.2023.15.4.091

Phonetics Speech Sci. 2023; 15(4):91-100

pISSN: 2005-8063, eISSN: 2586-5854

DOI: https://doi.org/10.13064/KSSS.2023.15.4.091

Speech Engineering/음성공학

주파수 대역별 잔향시간 추정을 위한 변형된 AWSSDR 방식^*

김민식¹, 김형순²^,^**

Modified AWSSDR method for frequency-dependent reverberation time estimation^*

Min Sik Kim¹, Hyung Soon Kim²^,^**

Author Information & Copyright ▼

¹부산대학교 컴퓨터및정보통신연구소

²부산대학교 전자공학과

¹Research Institute of Computer, Information and Communication, Pusan National University, Busan, Korea

²Department of Electronics Engineering, Pusan National University, Busan, Korea

^**Corresponding author : kimhs＠pusan.ac.kr

© Copyright 2023 Korean Society of Speech Sciences. This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Received: Nov 22, 2023; Revised: Dec 08, 2023; Accepted: Dec 08, 2023

Published Online: Dec 31, 2023

국문초록

잔향시간(reverberation time, T60)은 대표적인 음향 매개 변수로서, 잔향에 대한 정보를 제공한다. 동일한 공간이라도 주파수 대역에 따라 잔향이 미치는 영향은 다르기 때문에, 주파수 대역별(frequency-dependent, FD) T60은 음향환경에 대한 세부적인 정보를 제공하여 유용하게 사용될 수 있다. 하지만 음성신호로부터 T60을 추정하는 기존의 블라인드 T60 추정 방식들은 대부분 전 대역 T60 추정에 집중되어 있으며, 소수의 블라인드 FDT60 추정 방식들은 공통적으로 저주파 대역에서 열악한 성능을 보인다. 본 논문은 블라인드 FDT60 추정을 위해, 이전에 제안한 주의 집중 풀링 기반 스펙트럼 감쇠율의 가중 합(Attentive pooling based Weighted Sum of Spectral Decay Rates, AWSSDR) 방식을 변형하여 목표를 전 대역 T60에서 FDT60으로 확장하였다. 본 논문에서 제안한 방식은 ACE challenge의 평가데이터 셋에 대한 성능 평가 결과, 기존의 블라인드 FDT60 추정 방식들보다 우수한 성능을 달성하였으며, 특히, 모든 주파수 대역에서 일관성 있는 우수한 추정 성능을 보였다. 이는, 잔향의 물리적인 특성과 관련된 스펙트럼 감쇠율을 주파수 대역별로 처리하여, 음성신호로부터 FDT60에 대한 정보를 취합하는, AWSSDR 방식의 매커니즘이 주파수에 따라 변하는 잔향의 영향을 반영하여 FDT60 추정에 유용함을 보여준다.

Abstract

Reverberation time (T60) is a typical acoustic parameter that provides information about reverberation. Since the impacts of reverberation vary depending on the frequency bands even in the same space, frequency-dependent (FD) T60, which offers detailed insights into the acoustic environments, can be useful. However, most conventional blind T60 estimation methods, which estimate the T60 from speech signals, focus on fullband T60 estimation, and a few blind FDT60 estimation methods commonly show poor performance in the low-frequency bands. This paper introduces a modified approach based on Attentive pooling based Weighted Sum of Spectral Decay Rates (AWSSDR), previously proposed for blind T60 estimation, by extending its target from fullband T60 to FDT60. The experimental results show that the proposed method outperforms conventional blind FDT60 estimation methods on the acoustic characterization of environments (ACE) challenge evaluation dataset. Notably, it consistently exhibits excellent estimation performance in all frequency bands. This demonstrates that the mechanism of the AWSSDR method is valuable for blind FDT60 estimation because it reflects the FD variations in the impact of reverberation, aggregating information about FDT60 from the speech signal by processing the spectral decay rates associated with the physical properties of reverberation in each frequency band.

Keywords: 주파수 대역별 잔향시간; 블라인드 잔향시간 추정; 주의 집중 풀링

Keywords: frequency dependent T60; blind T60 estimation; attentive pooling

1. 서론

음향 매개 변수(acoustic parameter)는 실내 공간의 음향 특성과 음질에 대한 정보를 제공하여, 음성인식이나 음질개선 등의 다양한 음성 및 음향 신호처리 분야에서 유용하게 사용되고 있다(Chen et al., 2021; Giri et al., 2015; Tang & Manocha, 2021; Wang et al., 2021; Wu et al., 2017; Zhang et al., 2021). 잔향시간(reverberation time, T60)은 실내 공간의 잔향의 정도를 정량화하는 대표적인 음향 매개 변수로서, 수집된 음성의 품질과 음성인식 성능을 저하시키는 대표적인 요인 중 하나인, 잔향에 대한 정보를 제공한다.

T60은 음원이 차단된 후 음성의 에너지가 60 dB 감쇠하는데 소요되는 시간으로 정의되며(Kuttruff, 2019), 전통적으로 실내 임펄스 응답(room impulse response, RIR)으로부터 T60을 구하는 방법이 잘 정립되어 있다(Karjalainen et al., 2002). 하지만 RIR을 구하기 어려운 상황에서는 이러한 방법을 적용하는 것이 불가능하기 때문에, 오직 수집된 음성 신호로부터 T60을 추정하는 블라인드 T60 추정 방식들이 제시되고 있다(Bryan, 2020; Deng et al., 2020; Eaton & Naylor, 2015a; Eaton et al., 2013, 2016; Gamper & Tashev, 2018; Löllmann et al., 2015; Prego et al., 2015; Xiong et al., 2018; Zheng et al., 2022).

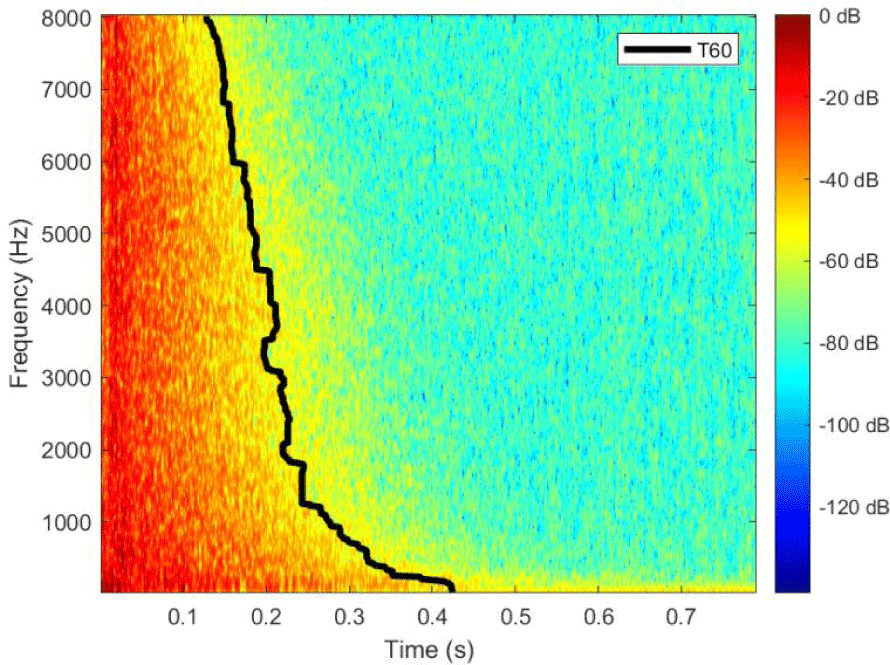
실내 공간에서 잔향을 결정하는 여러 흡수 반사 계수(absorption reflection coefficients)는 주파수에 따라 변하기 때문에, 잔향이 음성 신호에 미치는 영향과 T60은 주파수 대역마다 다르다(Wang et al., 2021). 그림 1은 실제 RIR에서 주파수 대역별로 스펙트럼이 다르게 감쇠하는 예를 보여준다. 구체적으로, 고주파 대역의 감쇠가 저주파 대역보다 빠르며, 즉 저주파 대역에서 고주파 대역으로 갈수록 T60이 짧아지는 경향이 있다. 이와 같은 잔향의 특성을 고려하면, 음향환경에 대한 세부적인 정보를 제공하는 주파수 대역별(frequency-dependent, FD) T60은 잔향의 영향을 처리하는 데에 있어, 전 대역(fullband) T60보다 더 유용하게 활용될 수 있다. FDT60은 전 대역 T60과 마찬가지로 RIR로부터 구할 수 있으며, 구체적으로 Eaton et al.(2016)이 설명한 바와 같이, RIR에 octave filterbank를 적용하여 주파수 대역별 RIR로 분해하고, 비선형 피팅 알고리즘(Karjalainen et al., 2002)을 적용하여 FDT60을 구하는 방법을 사용한다.

그림 1| Figure 1. 실제 RIR의 스펙트로그램과 주파수 종속 잔향시간의 예 | Example of a spectrogram of a real RIR and frequency-dependent reverberation time (FDT60) RIR, room impulse response.

Download Original Figure

하지만 대부분의 블라인드 T60 추정 방식은 이러한 잔향의 특성을 고려하지 않고, FDT60의 중요성은 강조되지 않았다. 오직 소수의 연구에서 블라인드 FDT60 추정이 이루어져 왔지만, 공통적으로 저주파 대역에서 매우 열악한 추정 성능을 보였다(Diether et al., 2015; Li et al., 2019; Löllmann & Vary, 2011; Löllmann et al., 2015; Xiong et al., 2018). Löllmann & Vary(2011)는 이러한 경향의 원인을 FDT60을 구하기 위해 적용하는 필터뱅크들이 낮은 주파수 대역에서 작은 대역폭을 갖기 때문이라 분석하였다.

이전 연구에서 우리는 주의 집중 풀링 기반 스펙트럼 감쇠율의 가중 합(Attentive pooling based Weighted Sum of Spectral Decay Rates, AWSSDR) 방식을 제안하였고, 블라인드 T60 추정 분야에서 벤치마크(benchmark)로 사용되는 ACE challenge의 평가데이터에 대해(Eaton et al., 2016), 가장 뛰어난 전 대역 T60 추정 성능을 달성하였다(Kim & Kim, 2022). 본 논문은 이러한 AWSSDR 방식을 일부 변형한 블라인드 FDT60 추정 방식을 제안한다.

본 논문의 구성은 다음과 같다. 서론에 이어 2장에서는 기존의 블라인드 FDT60 추정 방식을 설명하고, 3장에서는 AWSSDR 방식과, 우리가 제안하는 블라인드 FDT60 방식에 대해 자세히 소개한다. 그 후, 4장에서는 제안된 방식의 성능 평가를 위한 실험 및 결과를 제시하며, 5장에서 결론을 맺는다.

2. 기존의 블라인드 FDT60 추정 방식

2.1. ACE Challenge

Acoustic characterization of environments (ACE) challenge는 음향 매개 변수, 특히 T60과 직접-잔향 비율(direct-to-reverberation ratio, DRR)의 블라인드 추정을 위한 최첨단 알고리즘을 결정하고, 이 분야의 연구를 촉진시키기 위해 개최되었으며(Eaton et al., 2016), 지금까지도 여전히 블라인드 T60 추정의 평가를 위한 벤치마크로 사용되고 있다(Bryan, 2020; Deng et al., 2020; Gamper & Tashev, 2018; Xiong et al., 2018; Zheng et al., 2022). ACE challenge는 실제 잡음 환경에서의 잔향 음성 데이터 셋과, RIR로부터 구한 실제(ground truth) T60값을 제공하며, 전 대역 T60뿐만 아니라 FDT60도 실제 값을 제공하기 때문에, 블라인드 FDT60 추정 방식을 평가하는 데에도 유용하게 활용할 수 있다.

2.2. 주파수대역 정보를 활용한 ML 기반의 방식

Löllmann et al.(2015)이 제안한, 주파수 대역 정보를 활용한 최대 우도(maximum likelihood, ML) 기반의 방식은 ACE challenge에 참여한 여러 기관들 중 유일하게 FDT60 추정 성능을 보고하였다(Eaton et al., 2016). 이 방식은 음성신호를 여러 개의 주파수 대역으로 분해하고, 주파수 대역별로 ML 방식을 적용하여 FDT60을 추정한다. 그리고 ISO(2009)가 권장하는 대로 400에서 1250 Hz 범위에 대한 FDT60의 가중 합으로서 전 대역 T60을 추정하여, 추정오차의 분산 측면에서 기존의 ML 방식을 개선하였다.

게다가, 기존 블라인드 T60 추정 방식들의, 특히 저주파 대역에서 초래되는 FDT60에 대한 높은 추정오차 문제를 완화하기 위해, 고주파 대역의 더 신뢰도가 높은 FDT60으로부터 외삽하여 저주파 대역의 FDT60을 구하는 방식을 개발하였고, 이를 통해 특정한 잡음이 심한 경우를 제외하면 전 대역 T60에 준하는 FDT60 추정 성능을 달성하였다. 하지만 이 방식은 ACE challenge에 제출된 다른 방식들에 비해 전 대역 T60 추정 성능이 뛰어나지 않고, 그림 2에서 나타난 바와 같이, ACE challenge의 모든 평가데이터에 대한 FDT60 추정성능은 낮은 주파수대역(< 316 Hz)에서 여전히 열악한 성능을 보여준다(Eaton et al., 2017). 참고로, 각 주파수 대역별 추정오차를 보이기 위해 박스 플롯이 제시되었고, 그 값은 ( $T60^$ -T60)/T60 × 100 (%)으로 계산 되는, 상대적 추정오차로서, 좌측 y-축에 대응된다. 여기서, $T60^$ 은 T60의 추정 값을 의미한다. 박스 플롯의 각 박스에서, 중앙의 틈새는 중앙값을 나타내고, 박스의 가장자리는 25번째 백분위수와 75번째 백분위수를 나타낸다. 이상치(outlier)는 개별적으로 표시되었고, 각 박스 플롯의 수염(whisker)은 이상 치로 간주되지 않는 가장 극단적인 데이터 포인트까지 확장되었다. 또한, 다음 식의 Pearson 상관계수(correlation coefficient, ρ)가 같은 열에 파란색 엑스로 표시되었고, 그 값은 우측 y-축에 대응된다.

그림 2| Figure 2. ML 방식의 FDT60 추정 성능() | FDT60 estimation performance of ML method () ML, maximum likelihood.

Download Original Figure

ρ = ∑ n = 1 N (T60 n − T60 ˜) (T 60 n^− T60^˜) ∑ n = 1 N (T60 n − T 60 ˜) 2 ∑ n = 1 N (T60^n − T60^˜) 2

(1)

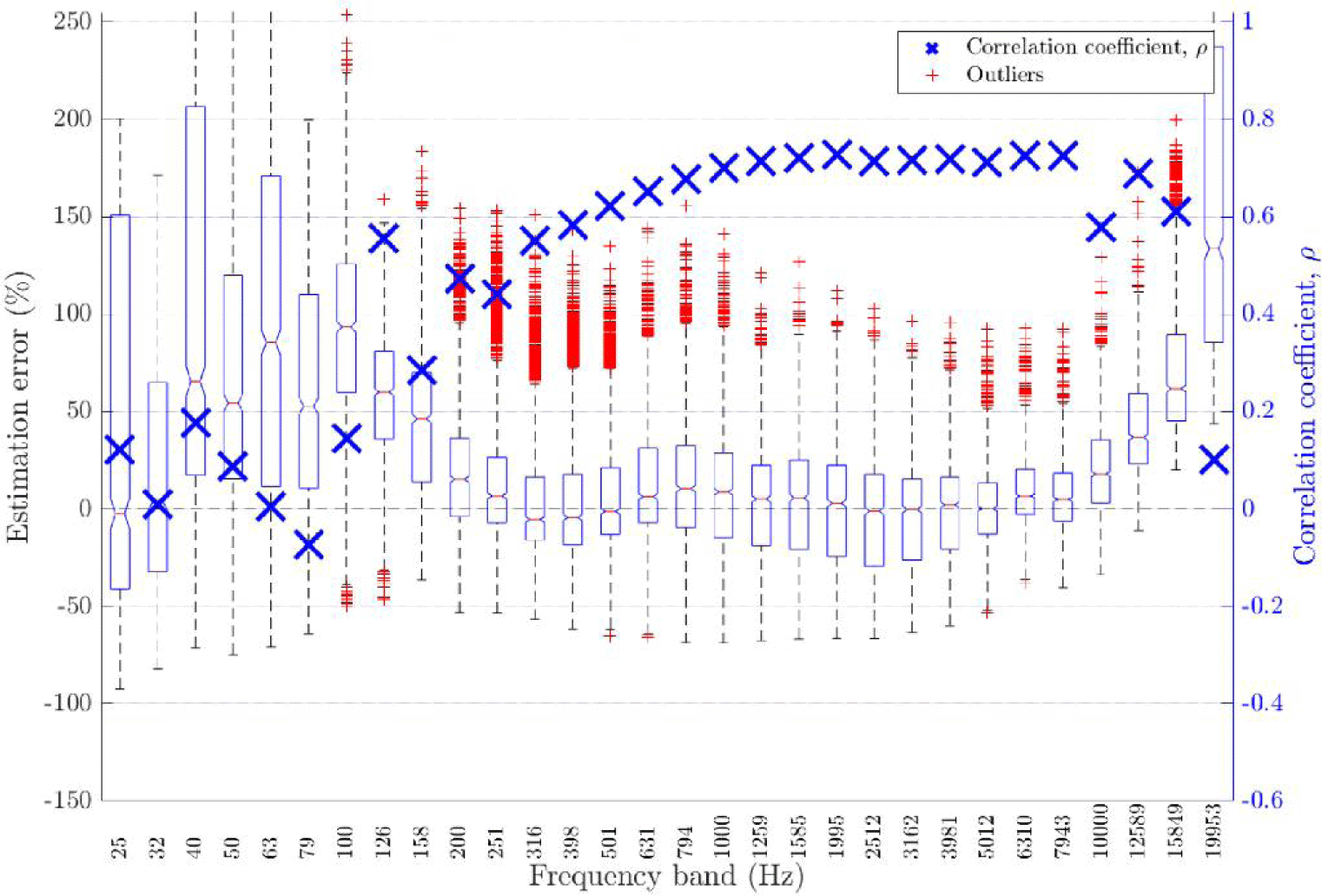
여기서, N은 결과데이터의 총 개수, T60_n과 $T60^n$ 은 각각 n번째 결과 데이터 T60의 실제 값과 추정 값, $T60 ˜$ 과 $T60^˜$ 은 각각 T60의 실제 값들과 추정 값들의 평균을 의미한다. 따라서 좌측 y-축에 대응되는 상대적 추정오차는 그 값들이 0에 가까이 분포할수록, 우측 y-축에 대응되는 Pearson 상관계수는 1에 가까울수록 즉, 클수록 T60 추정 성능이 뛰어남을 의미한다.

2.3. ROPE 방식

Xiong et al.(2018)은 블라인드 FDT60 추정을 위해 인공신경망(artificial neural network)에 기반한 room parameter estimator (ROPE) 방식을 제안하였다. 구체적으로, 음성신호에 감마톤(gammatone) 필터를 적용하여, 사람의 청각특성이 반영된 시간-주파수 도메인의 음향특징을 추출하고, 인접한 11개 프레임의 음향특징을 묶어서 이를 다층퍼셉트론(multi layer perceptron, MLP)의 입력으로 사용하였다. MLP는 이러한 입력특징이 이산화된 T60과 ELR(early-to-late reverberation ratio) class에 대해 매핑 되도록 훈련되었으며, 분류기(classifier)로서 매 프레임마다 T60 class를 예측하고, 최종적으로 시간에 대해 T60 class 대푯값의 평균을 구하여 음성신호의 T60을 추정한다.

ROPE 방식은 ACE challenge 평가데이터 셋에 대한 T60 추정 성능 평가에서 ACE challenge에 제출된 방식들 중 가장 뛰어난 방식에 준하는 성능을 달성하였으며, 훈련-테스트 데이터 간 RIR과 신호 대 잡음 비(signal-to-noise ratio, SNR), 음성 말뭉치 등의 차이에 강인한 성능을 달성하였다. 하지만, 기존 방식들과 마찬가지로 여전히 저주파 대역에서 성능 저하가 발생하였다. 그림 3은 박스플롯으로 나타낸 ROPE 방식의 블라인드 FDT60 및 전 대역 T60 추정 성능을 보여준다. 그림 2와 마찬가지로 각 주파수 대역별로 추정오차를 보이기 위해 박스플롯이 제시되었고 Pearson 상관계수가 함께 표시되었다. 다만, ROPE 방식은 T60뿐만 아니라, DRR 추정도 함께 수행하여 e_RT와 ρ_RT로 각각 추정오차와 Pearson 상관계수가 표시 되어 있으며, 좌측 y-축에는 상대적 추정오차가 아닌, $T60^$ -T60 (ms)의 추정오차가 대응된다.

그림 3| Figure 3. ROPE 방식의 FDT60 추정 성능() | FDT60 estimation performance of ROPE method () ROPE, ROom Parameter Estimator.

Download Original Figure

3. 제안 방식

3.1. 기본구조

다수의 분야에서 그러하듯이, 블라인드 T60 추정 분야에서도 딥러닝(deep learning)의 도입으로 기존의 신호처리 접근 방식들보다 우수한 성능을 달성하였다(Bryan, 2020; Deng et al., 2020; Gamper & Tashev, 2018; Zheng et al., 2022). 하지만 기존의 딥러닝에 기반한 블라인드 T60 추정 방식들은 단순히 심층신경망 구조에 의존하여 음성신호로부터 잔향의 특성을 포착해야 하고, 추정 과정에서 가변 입력 길이에 대한 추가적인 후처리를 필요로 하는 한계가 있다. 이러한 한계를 극복하기 위해 이전 연구에서 우리는 신호처리 접근법과 딥러닝 접근법을 결합한 AWSSDR 방식을 제안하였다.

3.1.1. 스펙트럼 감쇠율

스펙트럼 감쇠율(spectral decay rate, SDR)은 잔향의 물리적인 특성을 반영한 음향특징으로서 잔향의 영향을 나타내며, 시간 축을 따라 각 주파수 대역에 대한 로그 에너지 포락선(envelope)에 선형 최소 제곱(linear least squares, LLS) 피팅을 연속적으로 적용하여 구한다(Eaton et al., 2013). LLS 피팅이 모든 주파수 대역에 동일하게 적용되므로 주파수 인덱스를 생략하여 간결하게 설명하면, 길이 L의 로그 에너지 포락선 Y = [y₁,y₂,…,y_L ]^⊤가 주어졌을 때, 매 f_h 프레임마다 S개의 프레임을 묶어서 T개의 세그먼트 단위의 로그 에너지 포락선 집합 υ = [Y₁,Y₂,…,Y_T]^⊤을 구한다. 여기서, 위첨자 ⊤는 행렬 전치를 나타내고, τ번째 세그먼트 단위의 로그 에너지 포락선 Y_τ = [y_{τf_h}+1,y_{τf_h}+2,…,y_{τf_h+S}]^⊤에 LLS 피팅을 적용하여 총 T개의 SDR을 추출한다. LLS 피팅은 다음 식을 최소화하는 β_τ를 추정하여, Y_τ를 직선으로 근사화 한다.

L (β τ) = ‖ Y τ − X β τ ‖ 2

(2)

여기서 X는 독립 변수(시간 인덱스)의 행렬 즉,

X = [1, 2, 3, ⋯, S 1, 1, 1, ⋯, 1] ⊤

(3)

이고, $β τ = [β 1 τ, β 2 τ] ⊤$ 는 직선의 매개변수이다. $β 1 τ$ 는 직선의 기울기로서 τ번째 세그먼트의 SDR을 의미하고, 여기서 사용하지는 않지만 $β 2 τ$ 는 직선의 절편을 의미한다. 전통적인 신호처리 방식들에서는 선별과 제곱 평균 등의 통계치로 SDR을 집계하여, 블라인드 T60 추정에 활용하였다(Eaton & Naylor, 2015a; Eaton et al., 2013).

3.1.2. AWSSDR 방식

AWSSDR 방식은 여러 SDR에 불균형하게 분포한 T60에 대한 정보를 반영하기 위해서 soft decision 매커니즘을 도입하였다(Kim & Kim, 2022). 앞서 언급한 바와 같이, SDR은 잔향의 영향과 밀접한 관련이 있지만, 다른 요인들에 의해서도 크게 영향을 받는다. 예를 들어, 잡음이 심한 경우에는 SDR이 0에 가까운 값을 갖는 경향이 있는데 이는 잔향이 심한 경우와 유사한 현상이다. 잡음뿐만 아니라 SDR은 문맥과 발화자 등 다양한 요인에 영향을 받기 때문에, 모든 SDR이 T60 추정에 필요한 정보를 동일하게 포함하지는 않는다. 따라서 AWSSDR 방식은 T60 추정에 대한 정보의 중요도에 따라 각 SDR에 가중치를 할당한다. Vaswani et al.(2017)이 제안한 딥러닝 접근법의 어텐션(attention) 매커니즘을 적용하여 가중치를 학습하고, 이를 통해 SDR을 가중 합하여 발화 단위의 잔향 변별 특징으로서 블라인드 T60 추정에 활용한다.

그림 4는 음성신호로부터 T60을 추정하는 AWSSDR 방식의 과정을 간략하게 나타낸 것이다. 블라인드 T60 추정과정을 요약하면, SDR 추정단계에서 음성신호로부터 주파수 대역별 로그에너지 포락선을 구하고, 여기에 LLS 피팅을 적용하여 SDR 을 추정한다. 그 후, 주의 집중 풀링 단계에서 SDR을 가중치 추정 네트워크에 통과시켜 각 SDR에 가중치를 할당하고 이를 통해 집계된 가중 합 즉, AWSSDR을 구한다. 최종적으로, T60 매핑 단계에서 AWSSDR은 잔향 변별 특징으로서 T60 매핑 네트워크에 입력되어 T60 추정 값을 출력한다. 훈련단계에서는 두 종류의 네트워크 즉, 가중치 추정 네트워크와 T60 매핑 네트워크가 동시에 훈련된다.

그림 4| Figure 4. AWSSDR 방식의 흐름도 | Flowchart of AWSSDR method AWSSDR, Attentive pooling based Weighted Sum of Spectral Decay Rates.

Download Original Figure

3.2. AWSSDR을 활용한 블라인드 FDT60 추정 방식

3.2.1. 변형된 모델

앞서 설명한 AWSSDR 방식은 대부분의 블라인드 T60 추정 방식들과 마찬가지로 전 대역 T60 추정을 목표로 전체 시스템이 고안 및 구축 되었다. 본 논문에서는 FDT60 추정을 위해 전 대역 T60 추정에 사용된 AWSSDR 방식을 일부 변형하였다. T60 매핑 네트워크의 출력 노드의 수를, 목표로 하는 주파수 대역의 수와 동일하게 설정하여 각 출력 노드의 값이 대응되는 FDT60이 되도록 매핑하였다.

변형된 모델은 원래 AWSSDR 방식과 동일하게, 음성신호로부터 주파수 대역별로 SDR을 추정하여 가중치 추정 네트워크에 입력하고, 이를 통해 AWSSDR을 구한다. 구체적으로, 가중치 추정 네트워크에는 40개의 주파수대역에 대해 추출된 40×T의 SDR 시퀀스가 입력되어 각 SDR에 가중치가 할당된다. 그 후, 주파수 대역별로 SDR을 가중 합하여 40×1 크기의 발화단위 특징벡터인 AWSSDR을 생성한다. 이는 곧바로 변형된 모델의 T60 매핑 네트워크에 입력되어 FDT60 추정 값을 출력하며, 본 논문은 ROPE 방식과의 공정한 성능 비교를 위해서 40개의 주파수 대역에 대한 FDT60의 실제 값을 목표로 전체 네트워크를 학습하였다. 표 1은 본 논문에서 AWSSDR을 활용한 블라인드 FDT60 추정 방식의 세부적인 네트워크 구조를 보여준다.

표 1. | Table 1. AWSSDR 기반 FDT60 추정 방식의 구조 | The structure of the FDT60 estimation method based on AWSSDR

네트워크명	층 유형	세부 사양 I	세부 사양 II
가중치 추정 네트워크	Conv 1d	입력: 40×T, 출력: 80×T	Stride: 1, filter size: 11 padding size: 5 활성함수: LeakyReLU
	Conv 1d	입력: 80×T, 출력: 160×T
	Conv 1d	입력: 160×T, 출력: 320×T
	Conv 1d	입력: 320×T, 출력: 160×T
	Conv 1d	입력: 160×T, 출력: 80×T
	Conv 1d	입력: 80×T, 출력: 40×T
	Softmax	Row-wise 연산
T60 매핑 네트워크	Fully connected	입력: 40×1, 출력: 512×1, 활성함수: LeakyReLU
	Fully connected	입력: 512×1, 출력: 512×1, 활성함수: LeakyReLU
	Fully connected	입력: 512×1, 출력: 40×1, 활성함수: -

AWSSDR, Attentive pooling based Weighted Sum of Spectral Decay Rates.

Download Excel Table

3.2.2. FDT60의 실제 값

FDT60을 목표로 하는 AWSSDR 방식의 지도학습을 위해서는 FDT60의 실제 값이 필요하다. Karjalainen et al.(2002)은 비선형 피팅 알고리즘이 측정된 RIR에서의 비정상적인 노이즈 바닥에 대해 더 신뢰할 수 있는 결과를 생성한다는 것을 발견하였고, Eaton et al.(2016)은 RIR의 로그 매그니튜드 스펙트럼에 비선형 피팅 알고리즘을 적용하여 T60의 실제 값을 구하였다. 본 논문에서도 동일한 알고리즘을 사용하였고, 주파수 대역별 분석을 위해서 감마톤 필터를 적용하여 주파수 대역별로 RIR을 분해한 뒤, 비선형 피팅 알고리즘을 적용하여 FDT60의 실제 값을 구하고, 이를 훈련 및 평가에 활용하였다.

4. 성능평가

4.1. 실험환경

4.1.1. 훈련데이터

훈련데이터는 AWSSDR 방식의 SET-1 훈련데이터셋을 사용하였다(Kim & Kim, 2022). 구체적으로, SET-1 훈련데이터셋은 기존의 블라인드 T60 추정 방식들과의 공평한 비교를 위해 구축된 훈련데이터셋으로, ACE challenge에서 배포한 소프트웨어(Eaton & Naylor, 2015b)를 활용하여 음성신호에 잡음과 잔향을 부가하였다.

무잔향 음성 신호로 TIMIT corpus(Garofolo et al., 1993)와 잡음으로 Aurora-4 task(Parihar & Picone, 2002)에서 사용되는 6종류의 잡음을 사용하였고, RIR은 공개적으로 접근 가능한 RIR database로부터 전 대역 T60이 0.1초에서 1.5초 범위에 속하는 538개의 RIR을 선별하여 사용하였다. 모든 데이터의 샘플율은 16 kHz로 맞추어 훈련데이터셋을 구축하였고, [0, 10, 20] dB의 SNR 수준에 대해 모든 RIR과 잡음을 3번씩 부가하여 총 29,052 개의 잡음 및 잔향 음성신호로 훈련데이터셋이 구성된다.

4.1.2. 모델 훈련

음성신호에 매 8 ms마다 16 ms 크기의 Hamming 창 함수를 적용하여 구한 로그 멜 필터뱅크 에너지(log mel-filterbank energy, LMFE)를 로그 에너지 포락선으로, 매 두 프레임마다 40개 프레임 크기의 세그먼트에 대해 SDR을 추출하였고, Pytorch (Paszke et al., 2019)를 활용하여 SDR로부터 FDT60을 추정하는 전체 네트워크를 구축하였다. 모델 최적화에는 Adam optimizer를 사용하였고, 총 100 epoch만큼 훈련되는 동안 0.001의 초기 학습률로부터 시작해 50 epoch 이후부터는 매 epoch마다 0.99 배 감소된 학습률이 적용되도록 설정하였다. 미니-배치의 크기는 16으로, 그래디언트 누적을 적용하여 모델 훈련의 안정성을 높였다.

4.2. 실험 결과

표 2는 AWSSDR 기반의 블라인드 FDT60 추정 방식의 성능을 모든 주파수 대역에 대해 취합하여, 기존 AWSSDR 방식의 전 대역 T60 추정 성능과 비교한 것이다. 여기서 bias와 MSE 및 ρ는 ACE challenge에서 사용되는 평가 지표로, 각각 추정오차의 평균과, 제곱 오차의 평균 및 Pearson 상관계수를 의미한다. 표 2에서 보듯이 제안된 방식의 전 대역 T60 추정성능이 기존의 AWSSDR 방식에 비해서는 약간 뒤떨어진다. 다만 이는 전 대역 T60을 단일 목표로 추정하는 기존 AWSSDR 방식과 달리, 제안된 방식이 추구하는 목표가 잔향이 주파수 대역별로 다르게 미치는 영향을 반영하는, 다차원의 FDT60을 추정하는 것임을 고려할 때 충분히 이해되는 결과라고 판단된다.

표 2. | Table 2. AWSSDR 방식의 전 대역 T60과 FDT60 추정 성능 비교 | Performance comparison of AWSSDR method for fullband T60 and FDT60

T60 유형	Bias	MSE	ρ
전 대역 T60 (기존 방식)	–0.0091	0.0166	0.936
FDT60 (제안된 방식)	–0.0207	0.0224	0.921

MSE, mean squared error.

Download Excel Table

그림 5는 본 논문에서 제안된 방식의 FDT60 추정성능을 주파수 대역별로 나타냈으며, 기존의 블라인드 FDT60 추정 방식들처럼 박스플롯으로 주파수 대역별 추정오차를 나타내었다. 성능 비교를 위해 그림 5(a)에서는 그림 3의 Xiong et al.(2018)의 결과와 동일하게, 주파수 대역별로 –1,000 ms부터 1,000 ms 범위에서 추정오차를 나타내었으며, Pearson 상관계수와 root mean squared error(RMSE) 값을 각각 파란색과 초록색의 마커(marker)로 표시하였다. 앞에서 언급한 대로, Löllmann et al.(2015)은 그림 2에서와 같이 상대적 추정오차에 대한 박스플롯으로 추정성능을 보였다. 그림 2의 방식이 그림 3의 방식에 비해 성능이 떨어지므로 본 논문에서 제안된 방식과 직접적인 비교대상은 아니나, 그림 2의 방식과도 대략적으로 비교하기 위해, 그림 5(b)에 제안 방식의 실험 결과를 그림 2와 같이 상대적인 추정오차로 나타내었다. 다만 그림 5(b)에서 x축에 표시된 주파수 대역의 개수 및 중심 주파수는 그림 5(a)와 마찬가지로 직접 비교 대상인 그림 3과 동일하며, 그림 2와는 차이가 있다.

그림 5| Figure 5. AWSSDR 기반 블라인드 FDT60 추정 방식의 주파수 대역별 성능. (a) 추정오차 및 상관계수 (b) 상대적 추정오차 및 상관계수 | Performance of blind FDT60 estimation method based on AWSSDR according to frequency bands. (a) estimation error and correlation coefficient (b) relative estimation error and correlation coefficient

Download Original Figure

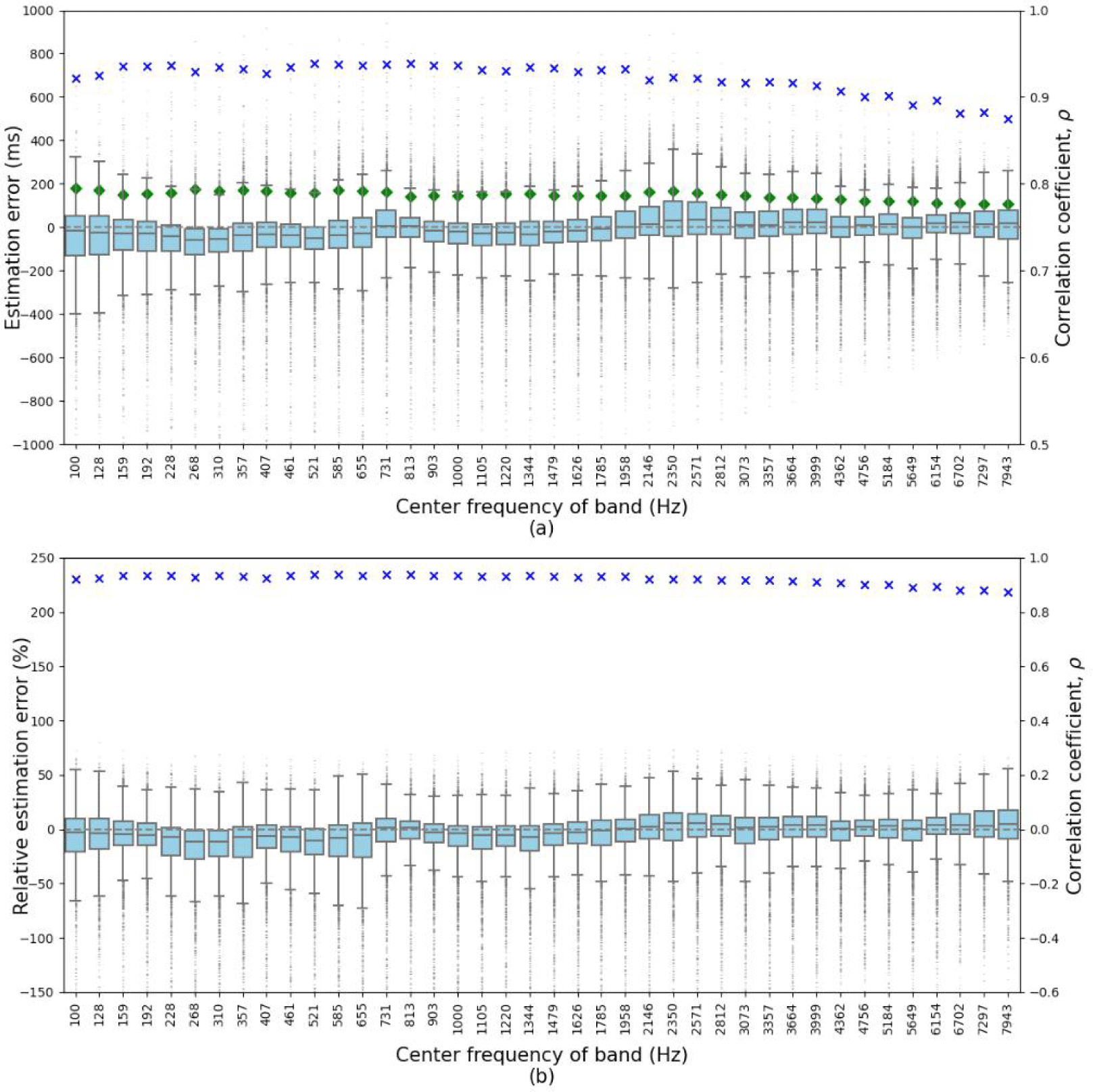
그림 3에서 상대적으로 추정성능이 좋은 주파수 대역의 추정오차가 –200 ms부터 200 ms 범위에 많이 분포한 반면, 본 논문에서 제안된 방식은 –100 ms부터 100 ms 범위에 많이 분포한다. 특히 그림 2에서 251 Hz 이하의 저주파 대역과 그림 3에서 407 Hz 이하의 저주파 대역에 대한 추정성능이 다른 주파수 대역들에 비해 매우 열악한 반면, 본 논문에서 제안된 방식은 모든 주파수 대역에서 일관성 있는 추정 성능을 보임을 알 수 확인할 수 있다.

5. 결론

본 논문에서는 블라인드 FDT60 추정을 위해, 이전에 블라인드 T60 추정을 위해 제안하였던 AWSSDR 방식의 목표를 전 대역 T60에서 FDT60으로 확장하였고, 이를 통해 기존의 블라인드 FDT60 추정 방식들에서 공통적으로 매우 열악한 성능을 보였던 저주파 대역에 대해 일관성 있는 우수한 추정 성능을 달성하였다. 이는, 잔향의 물리적인 특성과 관련된 스펙트럼 감쇠율을 주파수 대역별로 처리하여, 음성신호로부터 FDT60에 대한 정보를 취합하는, AWSSDR 방식의 매커니즘이 주파수에 따라 변하는 잔향의 영향을 반영하여 FDT60 추정에 유용함을 나타낸다.

Notes

^* 이 과제는 부산대학교 기본연구지원사업(2년)에 의하여 연구되었음.

^* 이 논문의 일부는 2023년 한국음성학회 봄 학술대회에서 발표되었음(Kim & Kim, 2023).

^* This work was supported by a 2-Year Research Grant of Pusan National University.

^* Part of this paper was presented at the 2023 Spring Conference of the Korean Society of Speech Sciences (Kim & Kim, 2023).

References/참고문헌

Bryan, N. J. (2020, May). Impulse response data augmentation and deep neural networks for blind room acoustic parameter estimation. Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (pp. 5000-5004). Barcelona, Spain.

Chen, S. J., Xia, W., & Hansen, J. H. L. (2021, December). Scenario aware speech recognition: Advancements for apollo fearless steps & chime-4 corpora. Proceedings of the IEEE Automatic Speech Recognition and Understanding Workshop (ASRU) (pp. 289-295). Cartagena, Colombia.

Deng, S., Mack, W., & Habets, E. A. P. (2020, October). Online blind reverberation time estimation using CRNNs. Proceedings of Interspeech (pp. 5061-5065). Shanghai, China.

Diether, S., Bruderer, L., Streich, A., & Loeliger, H. A. (2015, April). Efficient blind estimation of subband reverberation time from speech in non-diffuse environments. Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP) (pp. 743-747). South Brisbane, Australia.

Eaton, J., & Naylor, P. A. (2015a, October). Reverberation time estimation on the ACE corpus using the SDD method. Proceedings of the ACE Challenge Workshop, a Satellite of IEEE WASPAA (pp. 1-3). New Paltz, NY.

Eaton, J., & Naylor, P. A. (2015b, October). Acoustic characterization of environments (ACE) corpus software instructions. Proceedings of the ACE Challenge Workshop, a Satellite Event of IEEE WASPAA (pp. 1-5). New Paltz, NY, USA.

Eaton, J., Gaubitch, N. D., & Naylor, P. A. (2013, May). Noise-robust reverberation time estimation using spectral decay distributions with reduced computational cost. Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP) (pp. 161-165). Vancouver, Canada.

Eaton, J., Gaubitch, N. D., Moore, A. H., & Naylor, P. A. (2016). Estimation of room acoustic parameters: The ACE challenge. IEEE/ACM Transactions on Audio, Speech, and Language Processing, 24(10), 1681-1693.

Eaton, J., Gaubitch, N. D., Moore, A. H., & Naylor, P. A. (2017). Acoustic characterization of environments (ACE) challenge results technical report. arXiv. Retrieved from https://arxiv.org/abs/1606.03365

10.

Gamper, H., & Tashev, I. J. (2018, September). Blind reverberation time estimation using a convolutional neural network. Proceedings of the 16th International Workshop on Acoustic Signal Enhancement (pp. 136-140). Tokyo, Japan.

11.

Garofolo, J. S., Lamel, L. F., Fisher, W. M., Fiscus, J. G., Pallett, D. S., & Dahlgren, N. L. (1993). DARPA TIMIT: Acoustic-phonetic continuous speech corpus CD-ROM: NIST speech disc 1-1.1 (Technical Report NISTIR 4930). Gaithersburg, MD: National Institute Standards Technology.

12.

Giri, R., Seltzer, M. L., Droppo, J., & Yu, D. (2015, April). Improving speech recognition in reverberation using a room-aware deep neural network and multi-task learning. Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP) (pp. 5014-5018). South Brisbane, Australia.

13.

International Organization for Standardization. (2009). ISO 3382: Acoustics - Measurement of the reverberation time of rooms with reference to other acoustical parameters (2nd ed.). Geneva, Switzerland: International Organization for Standardization.

14.

Karjalainen, M., Ansalo, P., Mäkivirta, A., Peltonen, T., & Välimäki, V. (2002). Estimation of modal decay parameters from noisy response measurements. Journal of Audio Engineering Society, 50(11), 867-878.

15.

Kim, M. S., & Kim, H. S. (2022). Attentive pooling-based weighted sum of spectral decay rates for blind estimation of reverberation time. IEEE Signal Processing Letters, 29, 1639-1643.

16.

Kim, M. S., & Kim, H. S. (2023, June). Frequency-dependent T60 estimation using attentive pooling based weighted sum of spectral decay rates. Proceedings of the 2023 Spring Conference on Korean Society of Speech Sciences (KSSS). Seoul, Korea.

17.

Kuttruff, H. (2019). Room acoustics (6th ed.). Boca Raton, FL: CRC Press.

18.

Li, S., Schlieper, R., & Peissig, J. (2019, May). A hybrid method for blind estimation of frequency dependent reverberation time using speech signals. Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP) (pp. 211-215). Brighton, UK.

19.

Löllmann, H. W., & Vary, P. (2011, May). Estimation of the frequency dependent reverberation time by means of warped filter-banks. Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP) (pp. 309-312). Prague, Czech Republic.

20.

Löllmann, H. W., Brendel, A., Vary, P., & Kellermann, W. (2015, October). Single-channel maximum-likelihood T60 estimation exploiting subband information. Proceedings of the ACE Challenge Workshop, a Satellite of IEEE WASPAA (pp. 1-3). New Paltz, NY.

21.

Parihar, N., & Picone, J. (2002). Aurora working group: DSR front end LVCSR evaluation au/384/02 (Institute Signal Information Processing, Mississippi, MS, USA, Technical Report AU/384/02). Retrieved from https://isip.piconepress.com/publications/reports/aurora_frontend/2002/report_012202_v21.pdf

22.

Paszke, A., Gross, S., Massa, F., Lerer, A., Bradbury, J., Chanan, G., Killeen T, ... Chintala, S. (2019, December). PyTorch: An imperative style, high-performance deep learning library. Proceedings of the Advances in Neural Information Processing Systems 32 (NeurIPS 2019) (pp. 8024-8035). Vancouver, Canada.

23.

Prego, T. M., de Lima, A. A., Zambrano-López, R., & Netto, S. L. (2015, October). Blind estimators for reverberation time and direct-to-reverberant energy ratio using subband speech decomposition. Proceedings of the IEEE Workshop on Applications of Signal Processing to Audio and Acoustics (pp. 1-5). New Paltz, NY.

24.

Tang, Z., & Manocha, D. (2021). Scene-aware far-field automatic speech recognition. arXiv. Retrieved from https://arxiv.org/abs/2104.10757

25.

Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A. N., Kaiser, Ł., ... Polosukhin, I. (2017). Attention is all you need. Advances in Neural Information Processing Systems 30 (NIPS) (pp. 5998-6008). Long Beach, CA.

26.

Wang, H., Wu, B., Chen, L., Yu, M., Yu, J., Xu, Y., Zhang, S. X., ... Yu, D. (2021, August). Tecanet: Temporal-contextual attention network for environment-aware speech dereverberation. Proceedings of the Interspeech Conference (pp. 1109-1113). Brno, Czechia.

27.

Wu, B., Li, K., Yang, M., & Lee, C. H. (2017). A reverberation-time-aware approach to speech dereverberation based on deep neural networks. IEEE/ACM Transactions on Audio, Speech, and Language Processing, 25(1), 102-111.

28.

Xiong, F., Goetze, S., Kollmeier, B., & Meyer, B. T. (2018). Exploring auditory-inspired acoustic features for room acoustic parameter estimation from monaural speech. IEEE/ACM Transactions on Audio, Speech, and Language Processing, 26(10), 1809-1820.

29.

Zhang, Z., Li, X., Li, Y., Dong, Y., Wang, D., & Xiong, S. (2021, June). Neural noise embedding for end-to-end speech enhancement with conditional layer normalization. Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP) (pp. 7113-7117). Toronto, Canada.

30.

Zheng, K., Zheng, C., Sang, J., Zhang, Y., & Li, X. (2022). Noise-robust blind reverberation time estimation using noise-aware time–frequency masking. Measurement, 192, 110901.

31.

김민식, 김형순 (2023). 주의 집중 풀링 기반 스펙트럼 감쇠율의 가중합을 사용한 주파수 대역별 잔향시간 추정. 한국음성학회 2023 봄학술대회 논문집 (pp. 49).

주파수 대역별 잔향시간 추정을 위한 변형된 AWSSDR 방식*

국문초록

Abstract

1. 서론

2. 기존의 블라인드 FDT60 추정 방식

3. 제안 방식

4. 성능평가

5. 결론

Notes

References/참고문헌

주파수 대역별 잔향시간 추정을 위한 변형된 AWSSDR 방식^*